Funktionsterm (Herleitung)

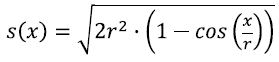
Zunächst müssen den Variablen in der Gleichung des Info Kosinussatzes

a2 = b2 + c2 − 2bc cos(α)     (*)

die richtigen Größen zugeordnet werden. a ist hier die Länge der Sehne s, während b und c hier jeweils den Radius r des Kreises bezeichnen. Der Winkel α = x/r ist der zur Sehne s gehörige Mittelpunktswinkel.
(Hilfe zu Winkeln im Bogenmaß: Info Bogenmaß)
Einsetzen in (*) liefert:

s2 = r2 + r2 − 2r2 cos(x/r)

Klammert man auf der rechten Seite der Gleichung den Faktor 2r2 aus, so ergibt sich:

s2 = 2r2 [1 − cos(x/r)]

Daraus folgt (Streckenlängen sind nicht negativ!):

s von x

Anmerkung

deriveDie Kurvengleichung für den allgemeinen Fall (auch P wird bewegt) lässt sich auch mit Hilfe des Kosinussatzes herleiten. In der hier herunterladbaren Derive-Datei ist die zugehörige Funktion der Sehnenlänge explizit angegeben und in verschieden dynamisch variierbaren graphischen Darstellungen (Parameterfunktion bzw. Funktion zweier Veränderlicher) ausgegeben.
Zurück Seitenanfang
  © Jürgen Roth
  http://juergen-roth.de